2. 円を基に黄金比を作成する

四角でない形でも、大きい順に分割数を見つけることができます。ここまでの方程式を元にさらに発展させていきますが、アーティスト自身の判断も必要になるでしょう。ドイツの画家 アルブレヒト・デューラー（Albrecht Dürer）は、五芒星を使って円の割合の計算方法を確立しました。

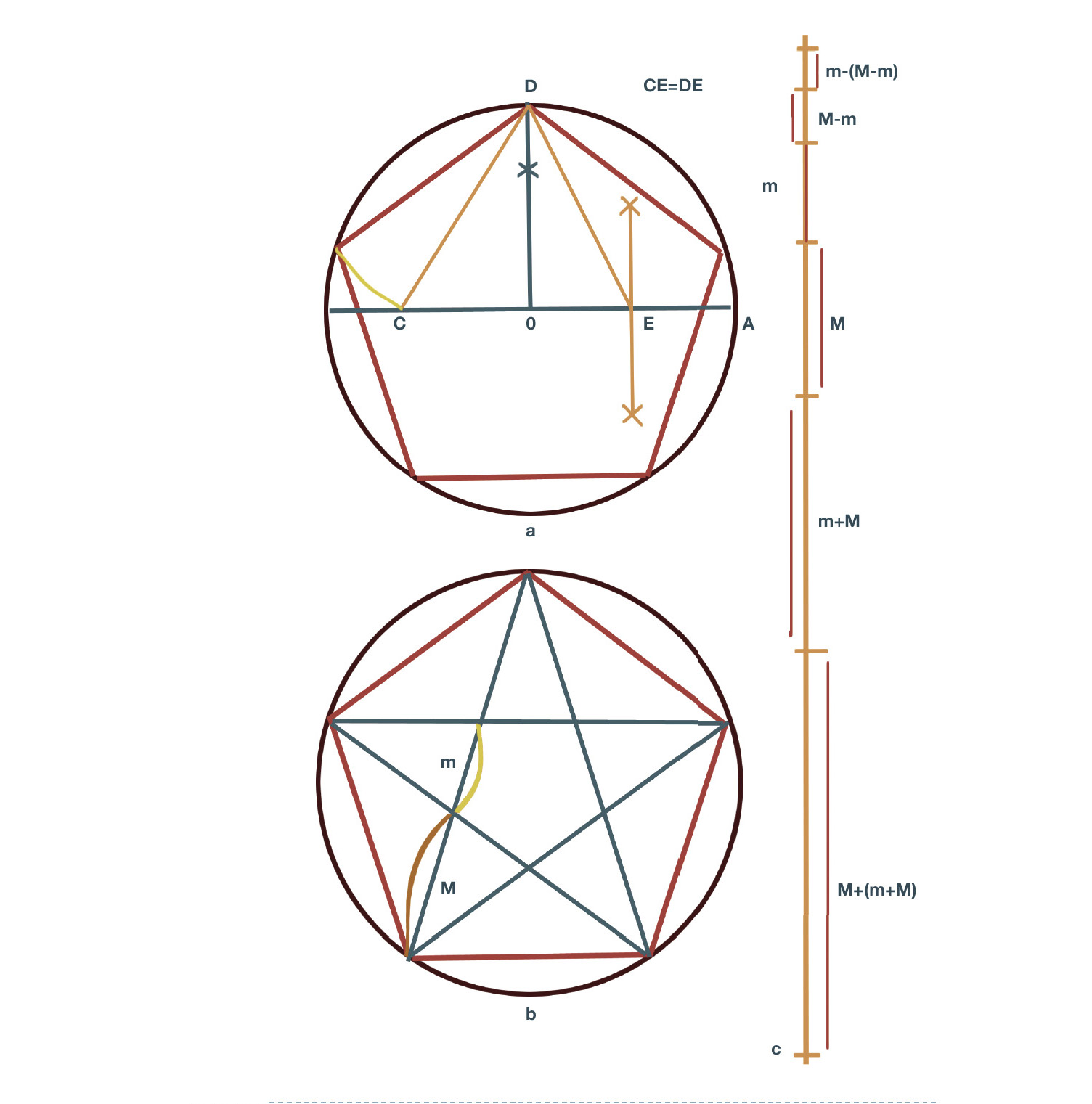
まず、正五角形を作成するため、以下の手順に従いましょう（図05）。円a の中心は 点O です。点A は円周上に、点E は OA線のちょうど中間（半径の半分）にあります。点D は、点O から垂直に上った円周上の交点です。点E を始点にコンパスでED間の距離を測り、コンパスを下へ回転させ、OA線の左に交差させ、点Cを作成します。

図05

次に、点D を始点にコンパスで DC 間の距離を測り、コンパスを上へ回転させて再び円周と交差させます。この円周上の点が、五角形の辺の最初の目印です。同じ測定方法で、この点を円周上の次の点に印を付けるための始点として使用します。再び点D にたどり着くまで、この操作を円周上で繰り返します。最後にそれぞれの印を直線で結んで正五角形を作成し、円内の交差線も結んで五芒星を作成します。

五芒星を構成するすべての対角線は、黄金比を示すセクションに円を分割します。絵に調和のとれたシステムを実現したいなら、黄金比の最初の2つのセクションを探してください（円b の M と m で表示）。これらの位置にオブジェクトを配置するだけで、理想的な視界と一致し、魅力的に見えるようになります。

五芒星の中に複数のオブジェクトを配置したい場合は、五芒星をいくつかの三角形の集まりと見なすか、次の計算方法で黄金比を探すとよいでしょう（正五角形の中の五芒星は、いくつかの二等辺三角形に分解できます）。

3. 二等辺三角形を基に黄金比を作成する

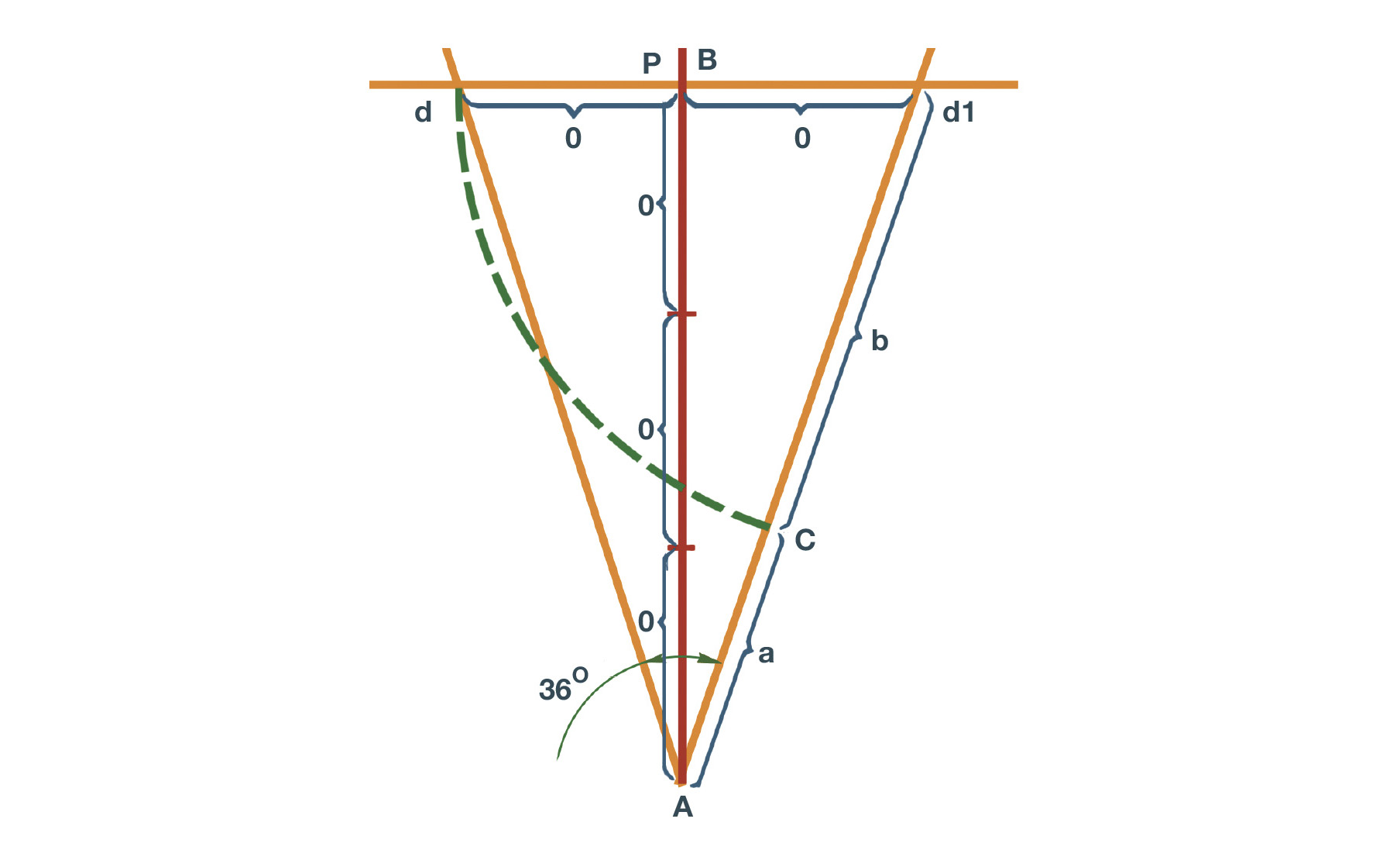
これまで見てきた基本的な比率の代数関数に従えば、二等辺三角形は比較的簡単です（図06）。まず、線AB を描き、これを3つのセクションに分割します（O）。その1つの長さを測り、点P からその分だけ 線AB と垂直に線を引きます。すると、長さが 2：3 の比となる線（Bと交わる2本の線）ができます。作成した終点（dとd1）から点Aに線を引くと、二等辺三角形になります。

点d1 を軸に三角形の底辺で長辺まで弧を描くと、黄金比の印を付けることができます（点C）。これを一歩進め、計算を応用すれば、直角三角形ABd を使用して、長方形の黄金比を割り出せるでしょう。

図06

4. 横長の長方形に黄金比を作成する：2つめの黄金比

プロポーションの精度をさらに高めるため、「2つめの黄金比」を見ていきましょう。これは元々、建築を拡張するときに発見されたもので、横長の絵に最適です。

先に結論を言うと、2つめの黄金比は、1つめの黄金比の線と絵の中心線の間になります。

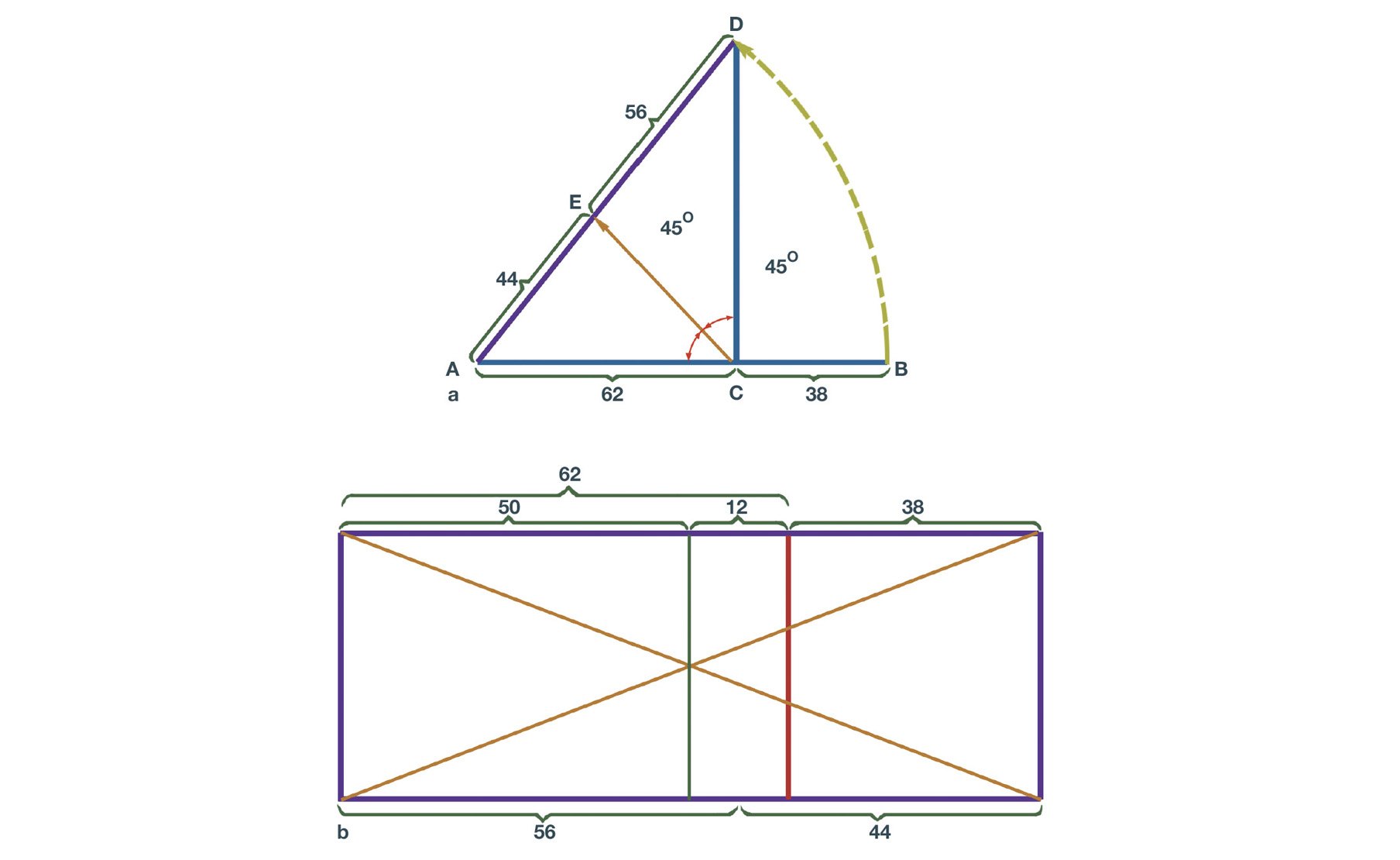
図07 はその求め方です。線AB は点Cで黄金比の割合に分割されています。まず、破線で示すように、線AB の長さを 45度回転させ、点D を見つけます。次に、線AD に黄金比の点C から 45度の直線を引くと、点E（2つめの黄金比）が見つかります。

これらの測定結果を横長の長方形の長さに当てはめると、56：44 の割合で、線を 2つめの黄金比に分割できます。

図07

以上が、数字を用いた黄金比のバリエーションになります。基本的な 長方形の黄金比、黄金螺旋、三分割法については、『デジタルアーティストが知っておくべきアートの原則 改訂版』をご覧ください。

編集部からのおすすめ： 色、構図.. アートのセオリーを学ぶ/再発見するには、書籍『デジタルアーティストが知っておくべきアートの原則 改訂版』そして、『続 デジタルアーティストが知っておくべきアートの原則』をおすすめします。